“An oz of prevention is value a pound of treatment” goes the outdated saying, reminding us that it is simpler to cease one thing from occurring within the first place than to restore the harm after it has occurred.

Within the period of synthetic intelligence (AI), this proverb underscores the significance of avoiding potential pitfalls, comparable to overfitting, by way of strategies like regularization.

On this article, we’ll uncover regularization by beginning with its basic rules to its utility utilizing Sci-kit Study(Machine Studying) and Tensorflow(Deep Studying) and witness its transformative energy with real-world datasets by evaluating these outcomes. Let’s begin!

 

What’s regularization?

 

Regularization is a important idea in machine studying and deep studying that goals to stop fashions from overfitting.

Overfitting occurs when a mannequin learns the coaching knowledge too nicely. The scenario reveals your mannequin is just too good to be true.

Let’s see what overfitting appears to be like like.

 

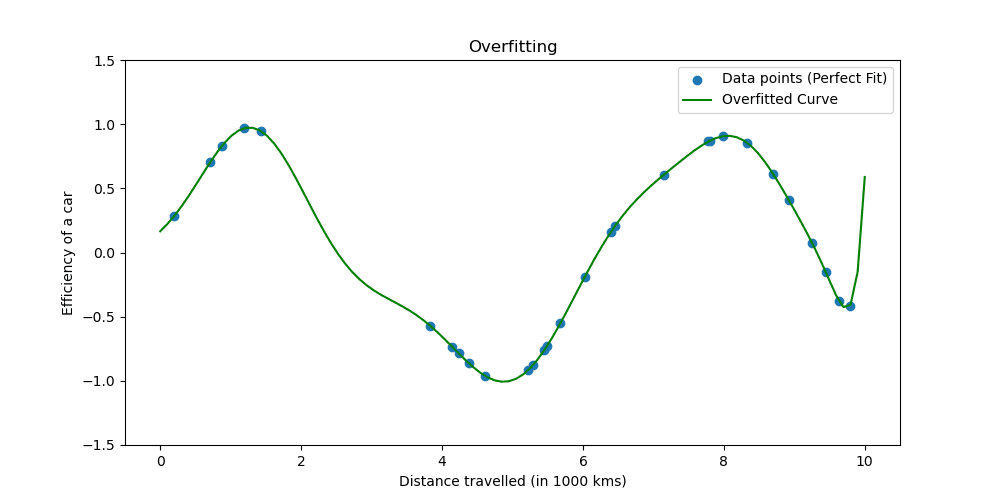
Regularization strategies modify the educational course of to simplify the mannequin, guaranteeing it performs nicely on coaching knowledge and generalizes nicely to new knowledge. We’ll discover two well-known methods of doing this.

 

Sort of Regularization

 

In machine studying, regularization is commonly utilized to linear fashions, comparable to linear and logistic regression. On this context, the commonest types of regularization are:

• L1 regularization (Lasso regression)
• L2 regularization (Ridge regression)

Lasso Regularization encourages the mannequin to make use of solely probably the most important options by permitting some coefficient values to be precisely zero, which could be significantly helpful for function choice.

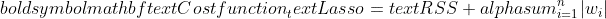
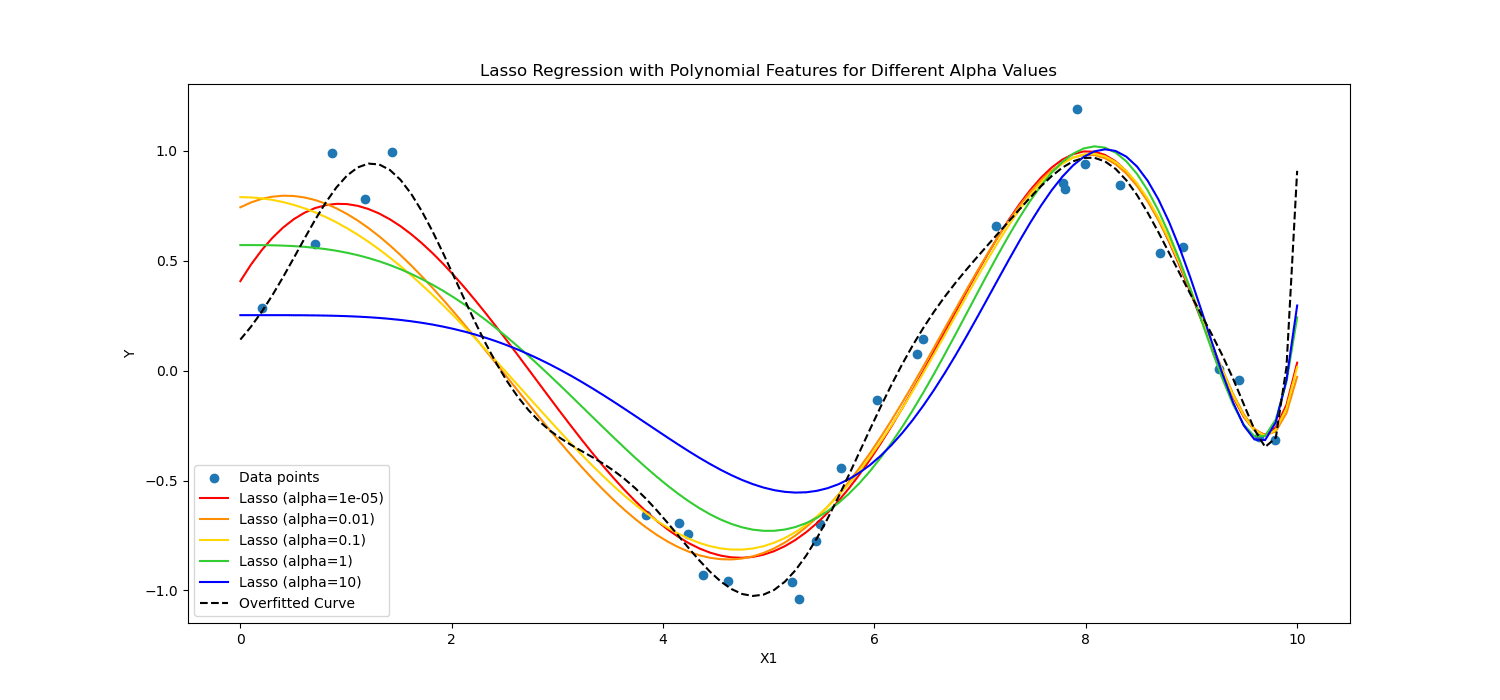
Then again, Ridge regularization discourages important coefficients by penalizing the sq. of their values.

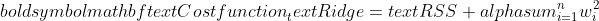
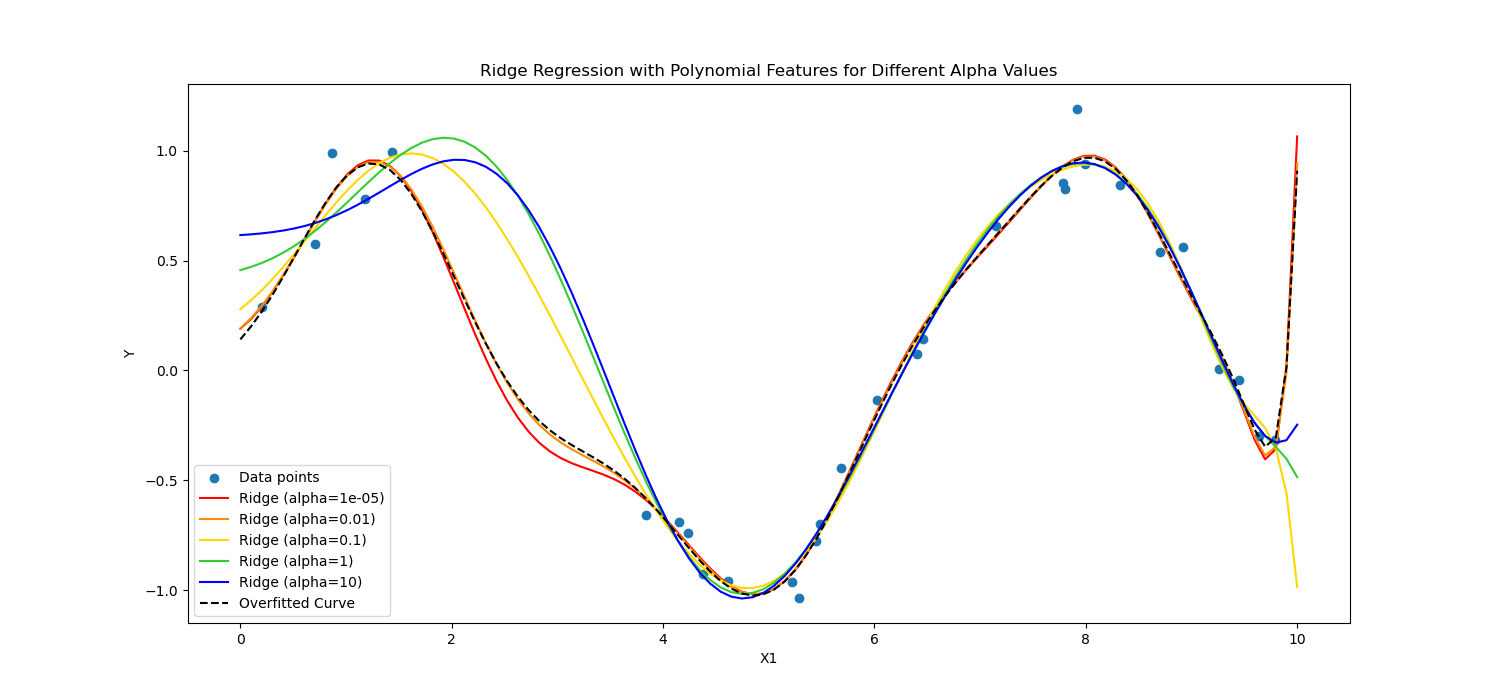
In brief, they calculated otherwise.

Let’s apply these to the cardiac affected person knowledge to see its energy In deep studying and machine studying.

 

The Energy of Regularization: Analyzing Cardiac Affected person Information

 

Now, we’ll apply regularization to research cardiac affected person knowledge to see the facility of regularization. You’ll be able to attain the dataset from right here.

To use machine studying, we’ll use Scikit-learn; to use deep studying, we’ll use TensorFlow. Let’s begin!

 

Regularization in Machine Studying

 

Scikit-learn is likely one of the hottest Python libraries for machine studying that gives easy and environment friendly knowledge evaluation and modeling instruments.

It contains implementations of assorted regularization strategies, significantly for linear fashions.

Right here, we’ll discover apply L1 (Lasso) and L2 (Ridge) regularization.

Within the following code, we’ll practice logistic regression utilizing Ridge(L2) and Lasso regularization (L1) strategies. On the finish, we’ll see the detailed report. Let’s see the code.

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report

# Assuming heart_data is already loaded
X = heart_data.drop('goal', axis=1)
y = heart_data['target']

# Break up the info into coaching and testing units
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Standardize the options
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.rework(X_test)

# Outline regularization values to discover
regularization_values = [0.001, 0.01, 0.1]

# Placeholder for storing efficiency metrics
performance_metrics = []

# Iterate over regularization values for L1 and L2
for C_value in regularization_values:
    # Prepare and consider L1 mannequin
    log_reg_l1 = LogisticRegression(penalty='l1', C=C_value, solver='liblinear')
    log_reg_l1.match(X_train_scaled, y_train)
    y_pred_l1 = log_reg_l1.predict(X_test_scaled)
    accuracy_l1 = accuracy_score(y_test, y_pred_l1)
    report_l1 = classification_report(y_test, y_pred_l1)
    performance_metrics.append(('L1', C_value, accuracy_l1))
    
    # Prepare and consider L2 mannequin
    log_reg_l2 = LogisticRegression(penalty='l2', C=C_value, solver='liblinear')
    log_reg_l2.match(X_train_scaled, y_train)
    y_pred_l2 = log_reg_l2.predict(X_test_scaled)
    accuracy_l2 = accuracy_score(y_test, y_pred_l2)
    report_l2 = classification_report(y_test, y_pred_l2)
    performance_metrics.append(('L2', C_value, accuracy_l2))

# Print the efficiency metrics for all fashions
print("Mannequin Efficiency Analysis:")
print("--------------------------------")
for metric in performance_metrics:
    reg_type, C_value, accuracy = metric
    print(f"Regularization: {reg_type}, C: {C_value}, Accuracy: {accuracy:.2f}")

 

Right here is the output.

 

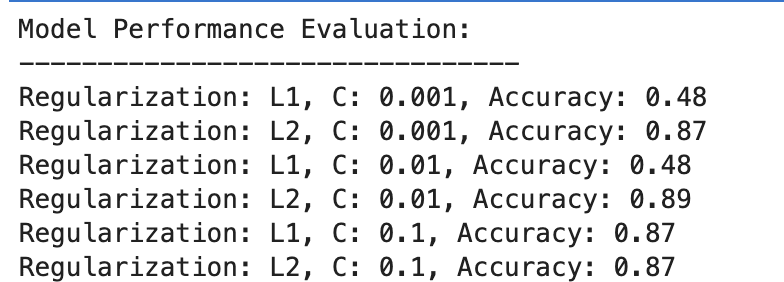
Let’s consider the outcome.

 

L1 Regularization

 

• At C=0.001, accuracy is notably low (48%). This reveals that the mannequin is underfitting. It reveals an excessive amount of regularization.
• As C will increase to 0.01, accuracy stays unchanged for L1, suggesting that the mannequin nonetheless suffers from underfitting or the regularization is just too robust.
• At C=0.1, accuracy improves considerably to 87%, displaying that decreasing the regularization power permits the mannequin to study higher from the info.

 

L2 Regularization

 

Throughout the board, L2 regularization performs constantly nicely, with accuracy at 87% for C=0.001 and barely greater at 89% for C=0.01, then stabilizing at 87% for C=0.1.

This implies that L2 regularization is usually extra forgiving and efficient for this dataset in logistic regression fashions, probably resulting from its nature.

 

Regularization in Deep Studying

 

A number of regularization strategies are utilized in deep studying, together with L1 (Lasso) and L2 (Ridge) regularization, dropout, and early stopping.

On this one, to repeat what we did within the machine studying instance earlier than, we’ll apply L1 and L2 regularization. Let’s outline an inventory of L1 and L2 regularization values this time.

Then, for all of those values, we’ll practice and consider our deep studying mannequin, and on the finish, we’ll assess the outcomes.

Let’s see the code.

from tensorflow.keras.regularizers import l1_l2
import numpy as np

# Outline an inventory/grid of L1 and L2 regularization values
l1_values = [0.001, 0.01, 0.1]
l2_values = [0.001, 0.01, 0.1]

# Placeholder for storing efficiency metrics
performance_metrics = []

# Iterate over all combos of L1 and L2 values
for l1_val in l1_values:
    for l2_val in l2_values:
        # Outline mannequin with the present mixture of L1 and L2
        mannequin = Sequential([
            Dense(128, activation='relu', input_shape=(X_train_scaled.shape[1],), kernel_regularizer=l1_l2(l1=l1_val, l2=l2_val)),
            Dropout(0.5),
            Dense(64, activation='relu', kernel_regularizer=l1_l2(l1=l1_val, l2=l2_val)),
            Dropout(0.5),
            Dense(1, activation='sigmoid')
        ])
        
        mannequin.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
        
        # Prepare the mannequin
        historical past = mannequin.match(X_train_scaled, y_train, validation_split=0.2, epochs=100, batch_size=10, verbose=0)
        
        # Consider the mannequin
        loss, accuracy = mannequin.consider(X_test_scaled, y_test, verbose=0)
        
        # Retailer the efficiency together with the regularization values
        performance_metrics.append((l1_val, l2_val, accuracy))

# Discover one of the best performing mannequin
best_performance = max(performance_metrics, key=lambda x: x[2])
best_l1, best_l2, best_accuracy = best_performance

# After the loop, to print all efficiency metrics
print("All Mannequin Performances:")
print("L1 Worth | L2 Worth | Accuracy")
for metrics in performance_metrics:
    print(f"{metrics[0]:<8} | {metrics[1]:<8} | {metrics[2]:.3f}")

# After discovering one of the best efficiency, to print one of the best mannequin particulars
print("nBest Mannequin Efficiency:")
print("----------------------------")
print(f"Finest L1 worth: {best_l1}")
print(f"Finest L2 worth: {best_l2}")
print(f"Finest accuracy: {best_accuracy:.3f}")

 

Right here is the output.

 

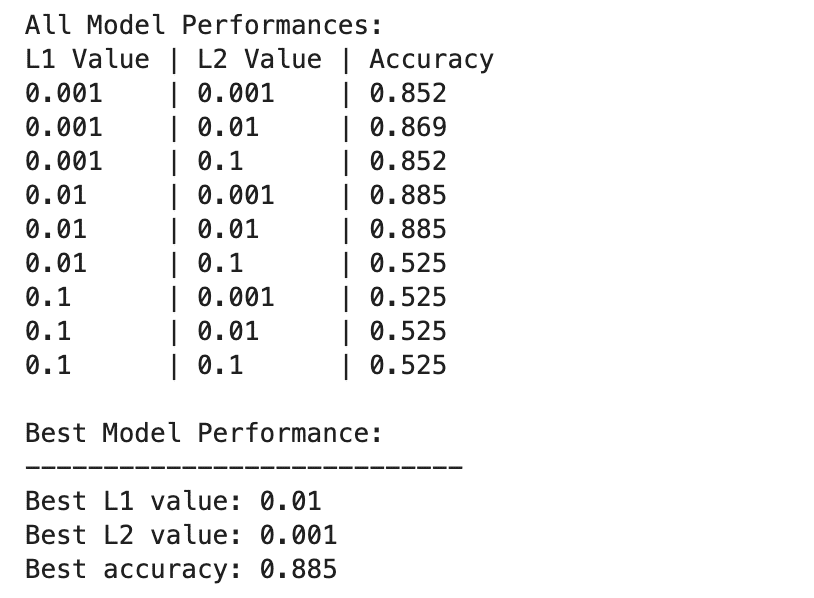
The deep studying mannequin performances range extra broadly throughout completely different combos of L1 and L2 regularization values.

The most effective efficiency is noticed at L1=0.01 and L2=0.001, with an accuracy of 88.5%, which signifies a balanced regularization that stops overfitting whereas permitting the mannequin to seize the underlying patterns within the knowledge.

Larger regularization values, particularly at L1=0.1 or L2=0.1, drastically scale back mannequin accuracy to 52.5%, suggesting that an excessive amount of regularization severely limits the mannequin’s studying capability.

 

Machine Studying & Deep Studying in Regularization

 

Let’s examine the outcomes between Machine Studying and Deep Studying.

Effectiveness of Regularization: Each in machine studying and deep studying contexts, applicable regularization helps mitigate overfitting, however extreme regularization results in underfitting. The optimum regularization power varies, with deep studying fashions probably requiring a extra nuanced steadiness resulting from their greater complexity.

Efficiency: The most effective-performing machine studying mannequin (L2 with C=0.01, 89% accuracy) and the best-performing deep studying mannequin (L1=0.01, L2=0.001, 88.5% accuracy) obtain comparable accuracies, demonstrating that each approaches could be successfully regularized to realize excessive efficiency on this dataset.

Regularization Technique: L2 regularization seems to be simpler and fewer delicate to the selection of C in logistic regression fashions, whereas a mixture of L1 and L2 regularization gives one of the best lead to deep studying, providing a steadiness between function choice and weight penalization.

The selection and power of regularization needs to be rigorously tuned to steadiness studying complexity with the danger of overfitting or underfitting.

 

Conclusion

 

All through this exploration, we have demystified regularization, displaying its function in stopping overfitting and guaranteeing our fashions generalize nicely to unseen knowledge.

Making use of regularization strategies will deliver you nearer to proficiency in machine studying and deep studying, solidifying your knowledge scientist toolset.

Go into the info initiatives and check out regularizing your knowledge in numerous situations, comparable to Supply Length Prediction. We used each Machine Studying and Deep Studying fashions on this knowledge undertaking. Nevertheless, in the long run, we additionally talked about that there is perhaps room for enchancment. So why don’t you attempt regularization over there and see if it helps?

Nate Rosidi is an information scientist and in product technique. He is additionally an adjunct professor instructing analytics, and is the founding father of StrataScratch, a platform serving to knowledge scientists put together for his or her interviews with actual interview questions from prime firms. Nate writes on the most recent traits within the profession market, provides interview recommendation, shares knowledge science initiatives, and covers all the things SQL.