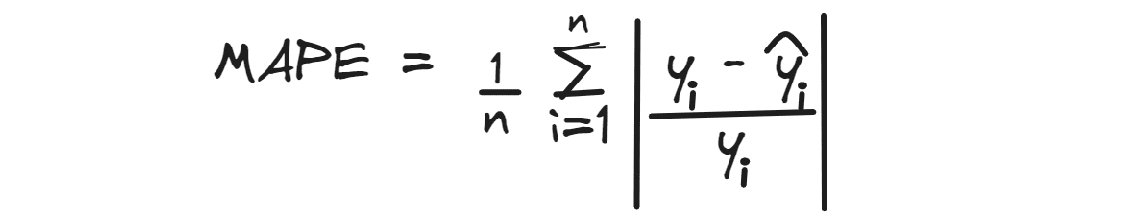
Picture by Creator

While you’re familiarizing your self with the unsupervised studying paradigm, you will study clustering algorithms.

The aim of clustering is usually to grasp patterns within the given unlabeled dataset. Or it may be to discover teams within the dataset—and label them—in order that we are able to carry out supervised studying on the now-labeled dataset. This text will cowl the fundamentals of hierarchical clustering.

What Is Hierarchical Clustering?

Hierarchical clustering algorithm goals at discovering similarity between situations—quantified by a distance metric—to group them into segments referred to as clusters.

The aim of the algorithm is to search out clusters such that information factors in a cluster are extra related to one another than they’re to information factors in different clusters.

There are two frequent hierarchical clustering algorithms, every with its personal strategy:

Agglomerative Clustering
Divisive Clustering

Agglomerative Clustering

Suppose there are n distinct information factors within the dataset. Agglomerative clustering works as follows:

Begin with n clusters; every information level is a cluster in itself.
Group information factors collectively primarily based on similarity between them. That means related clusters are merged relying on the space.
Repeat step 2 till there may be just one cluster.

Divisive Clustering

Because the identify suggests, divisive clustering tries to carry out the inverse of agglomerative clustering:

All of the n information factors are in a single cluster.
Divide this single giant cluster into smaller teams. Observe that the grouping collectively of knowledge factors in agglomerative clustering is predicated on similarity. However splitting them into totally different clusters is predicated on dissimilarity; information factors in numerous clusters are dissimilar to one another.
Repeat till every information level is a cluster in itself.

Distance Metrics

As talked about, the similarity between information factors is quantified utilizing distance. Generally used distance metrics embrace the Euclidean and Manhattan distance.

For any two information factors within the n-dimensional characteristic area, the Euclidean distance between them given by:

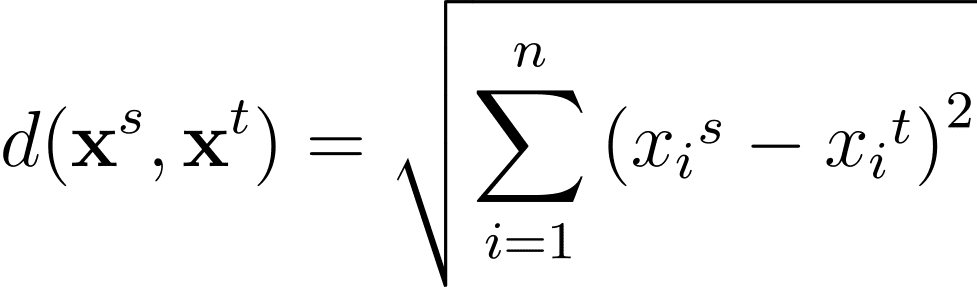
One other generally used distance metric is the Manhattan distance given by:

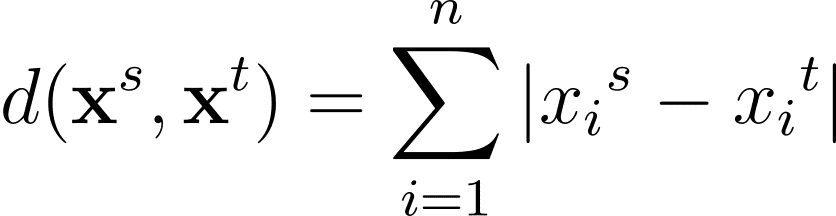
The Minkowski distance is a generalization—for a normal p >= 1—of those distance metrics in an n-dimensional area:

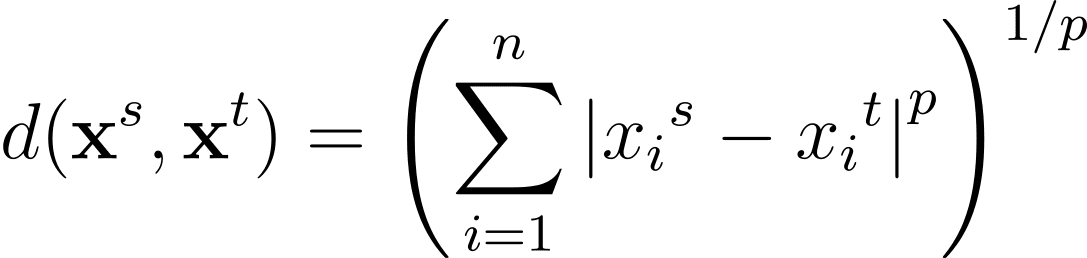
Distance Between Clusters: Understanding Linkage Standards

Utilizing the space metrics, we are able to compute the space between any two information factors within the dataset. However you additionally have to outline a distance to find out “how” to group collectively clusters at every step.

Recall that at every step in agglomerative clustering, we choose the two closest teams to merge. That is captured by the linkage criterion. And the generally used linkage standards embrace:

Single linkage
Full linkage
Common linkage
Ward’s linkage

Single Linkage

In single linkage or single-link clustering, the space between two teams/clusters is taken because the smallest distance between all pairs of knowledge factors within the two clusters.

Full Linkage

In full linkage or complete-link clustering, the space between two clusters is chosen because the largest distance between all pairs of factors within the two clusters.

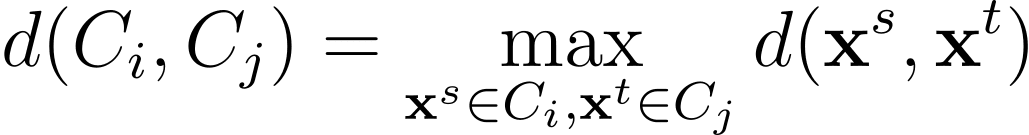
Common Linkage

Generally common linkage is used which makes use of the typical of the distances between all pairs of knowledge factors within the two clusters.

Ward’s Linkage

Ward’s linkage goals to reduce the variance inside the merged clusters: merging clusters ought to reduce the general improve in variance after merging. This results in extra compact and well-separated clusters.

The gap between two clusters is calculated by contemplating the improve within the whole sum of squared deviations (variance) from the imply of the merged cluster. The thought is to measure how a lot the variance of the merged cluster will increase in comparison with the variance of the person clusters earlier than merging.

Once we code hierarchical clustering in Python, we’ll use Ward’s linkage, too.

What Is a Dendrogram?

We are able to visualize the results of clustering as a dendrogram. It’s a hierarchical tree construction that helps us perceive how the information factors—and subsequently clusters—are grouped or merged collectively because the algorithm proceeds.

Within the hierarchical tree construction, the leaves denote the situations or the information factors within the information set. The corresponding distances at which the merging or grouping happens might be inferred from the y-axis.

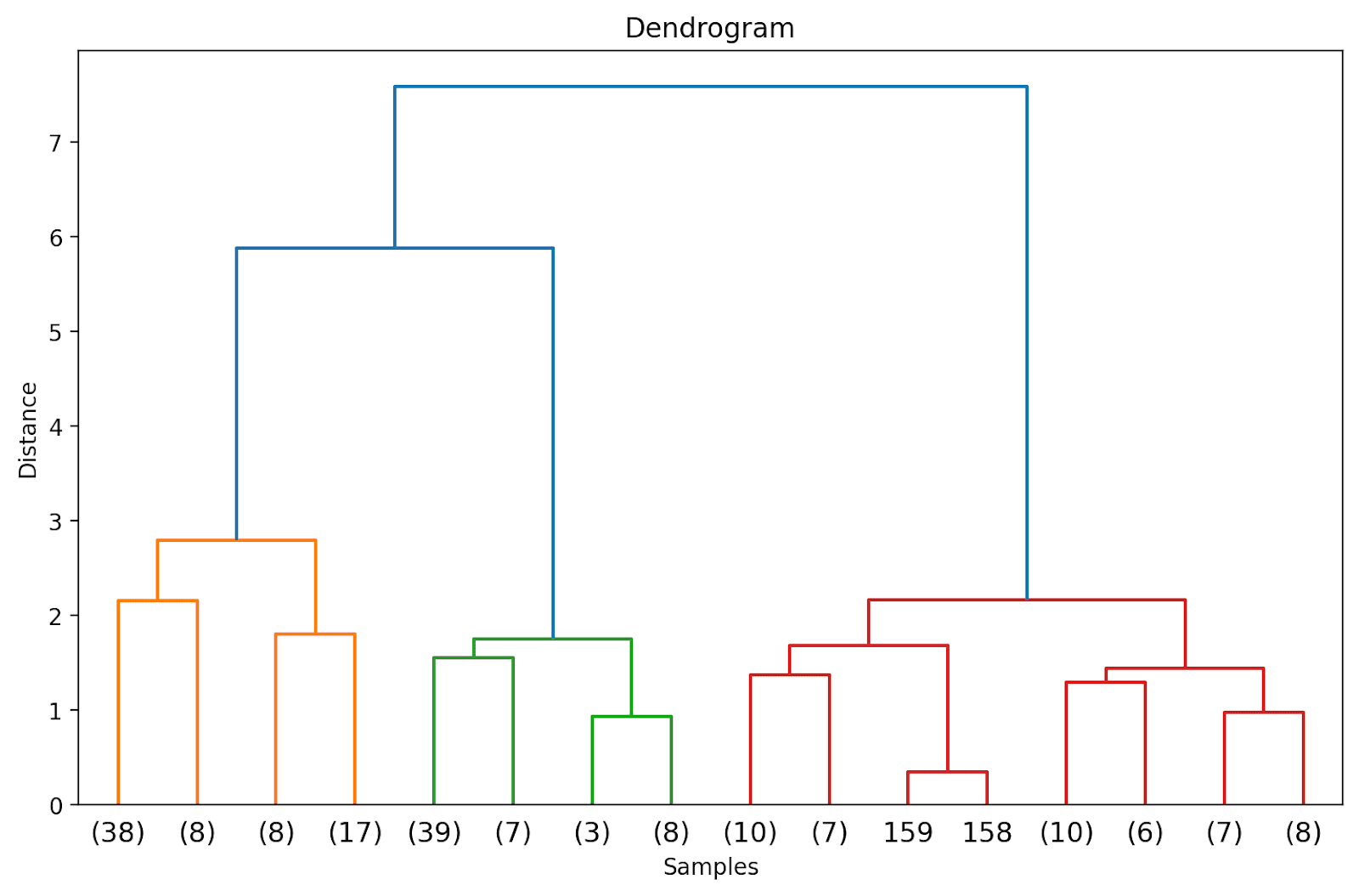
Pattern Dendrogram | Picture by Creator

As a result of the kind of linkage determines how the information factors are grouped collectively, totally different linkage standards yield totally different dendrograms.

Primarily based on the space, we are able to use the dendrogram—lower or slice it at a particular level—to get the required variety of clusters.

In contrast to some clustering algorithms like Ok-Means clustering, hierarchical clustering doesn’t require you to specify the variety of clusters beforehand. Nonetheless, agglomerative clustering might be computationally very costly when working with giant datasets.

Hierarchical Clustering in Python with SciPy

Subsequent, we’ll carry out hierarchical clustering on the built-in wine dataset—one step at a time. To take action, we’ll leverage the clustering bundle—scipy.cluster—from SciPy.

Step 1 – Import Vital Libraries

First, let’s import the libraries and the mandatory modules from the libraries scikit-learn and SciPy:

# imports
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_wine
from sklearn.preprocessing import MinMaxScaler
from scipy.cluster.hierarchy import dendrogram, linkage

Step 2 – Load and Preprocess the Dataset

Subsequent, we load the wine dataset right into a pandas dataframe. It’s a easy dataset that’s a part of scikit-learn’s datasets and is useful in exploring hierarchical clustering.

# Load the dataset
information = load_wine()
X = information.information

# Convert to DataFrame
wine_df = pd.DataFrame(X, columns=information.feature_names)

Let’s examine the primary few rows of the dataframe:

wine_df.head()

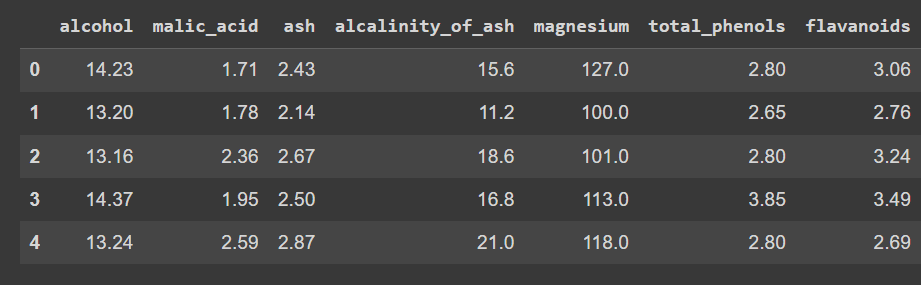
Truncated output of wine_df.head()

Discover that we’ve loaded solely the options—and never the output label—in order that we are able to peform clustering to find teams within the dataset.

Let’s examine the form of the dataframe:

print(wine_df.form)

There are 178 information and 14 options:

Output >>> (178, 14)

As a result of the information set comprises numeric values which can be unfold throughout totally different ranges, let’s preprocess the dataset. We’ll use MinMaxScaler to remodel every of the options to tackle values within the vary [0, 1].

# Scale the options utilizing MinMaxScaler
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(X)

Step 3 – Carry out Hierarchical Clustering and Plot the Dendrogram

Let’s compute the linkage matrix, carry out clustering, and plot the dendrogram. We are able to use linkage from the hierarchy module to calculate the linkage matrix primarily based on Ward’s linkage (set methodology to ‘ward’).

As mentioned, Ward’s linkage minimizes the variance inside every cluster. We then plot the dendrogram to visualise the hierarchical clustering course of.

# Calculate linkage matrix
linked = linkage(X_scaled, methodology='ward')

# Plot dendrogram
plt.determine(figsize=(10, 6),dpi=200)
dendrogram(linked, orientation='prime', distance_sort='descending', show_leaf_counts=True)
plt.title('Dendrogram')
plt.xlabel('Samples')
plt.ylabel('Distance')
plt.present()

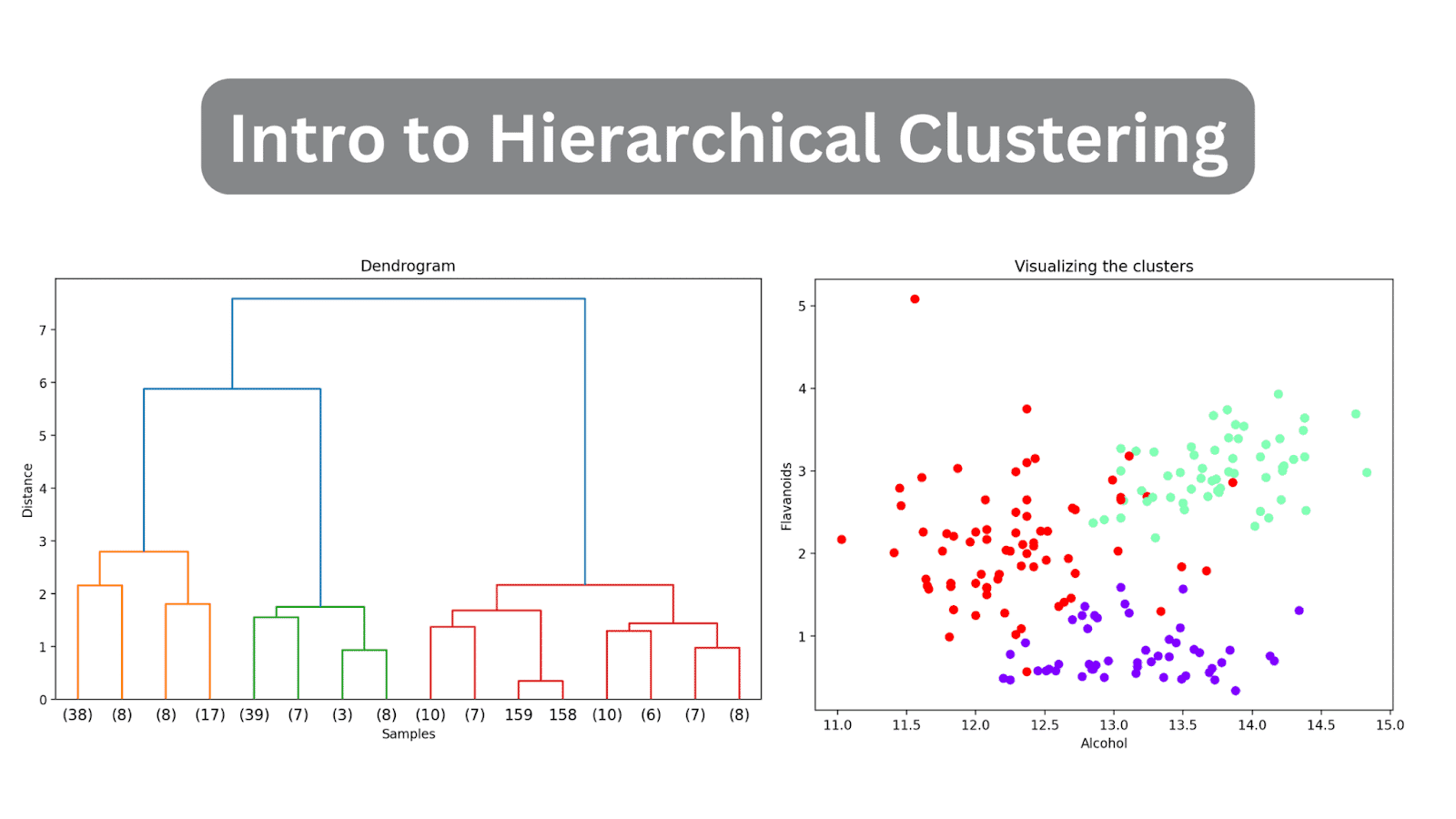
As a result of we have not (but) truncated the dendrogram, we get to visualise how every of the 178 information factors are grouped collectively right into a single cluster. Although that is seemingly troublesome to interpret, we are able to nonetheless see that there are three totally different clusters.

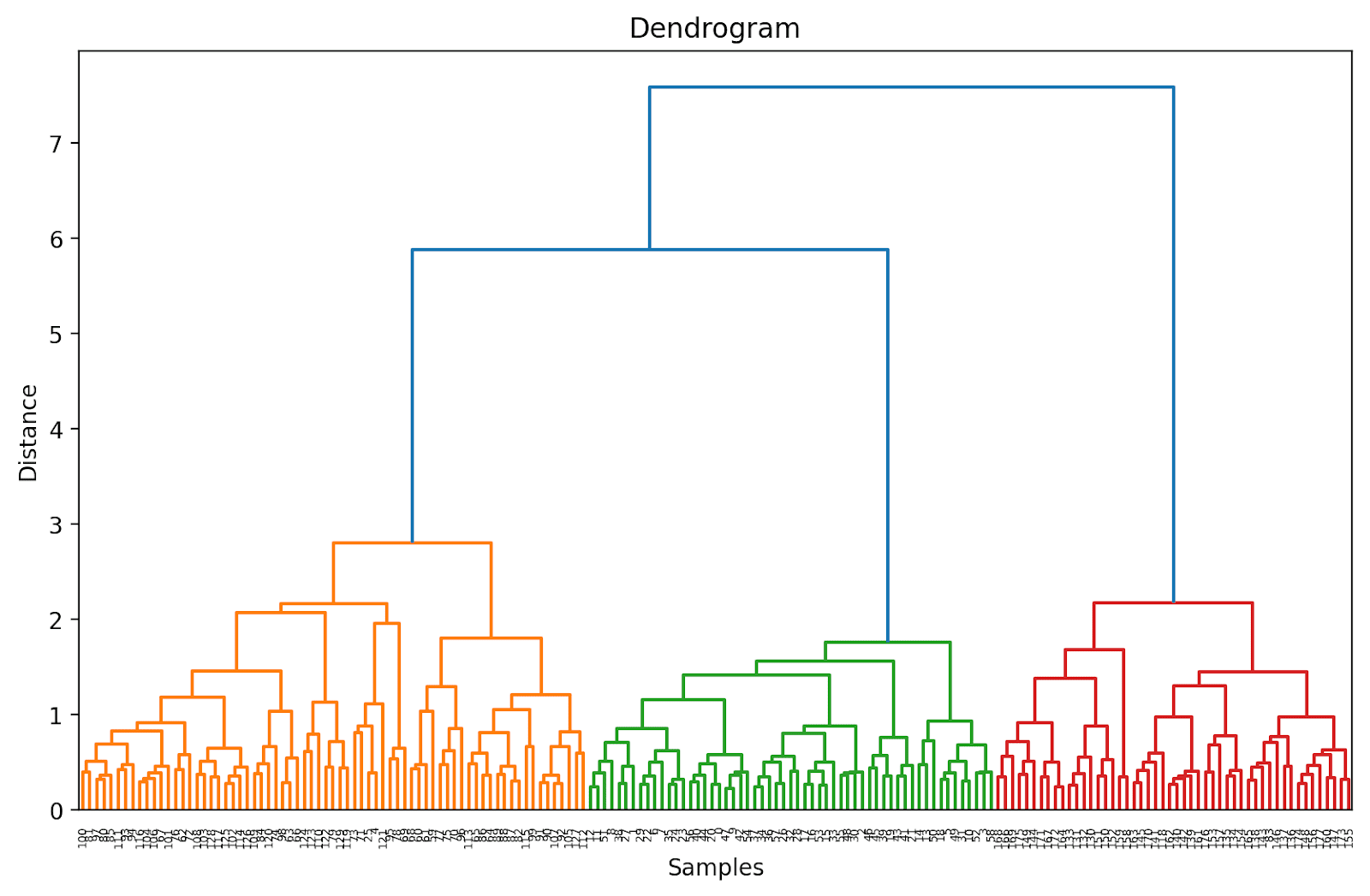
Truncating the Dendrogram for Simpler Visualization

In observe, as an alternative of your entire dendrogram, we are able to visualize a truncated model that is simpler to interpret and perceive.

To truncate the dendrogram, we are able to set truncate_mode to ‘degree’ and p = 3.

# Calculate linkage matrix
linked = linkage(X_scaled, methodology='ward')

# Plot dendrogram
plt.determine(figsize=(10, 6),dpi=200)
dendrogram(linked, orientation='prime', distance_sort='descending', truncate_mode='degree', p=3, show_leaf_counts=True)
plt.title('Dendrogram')
plt.xlabel('Samples')
plt.ylabel('Distance')
plt.present()

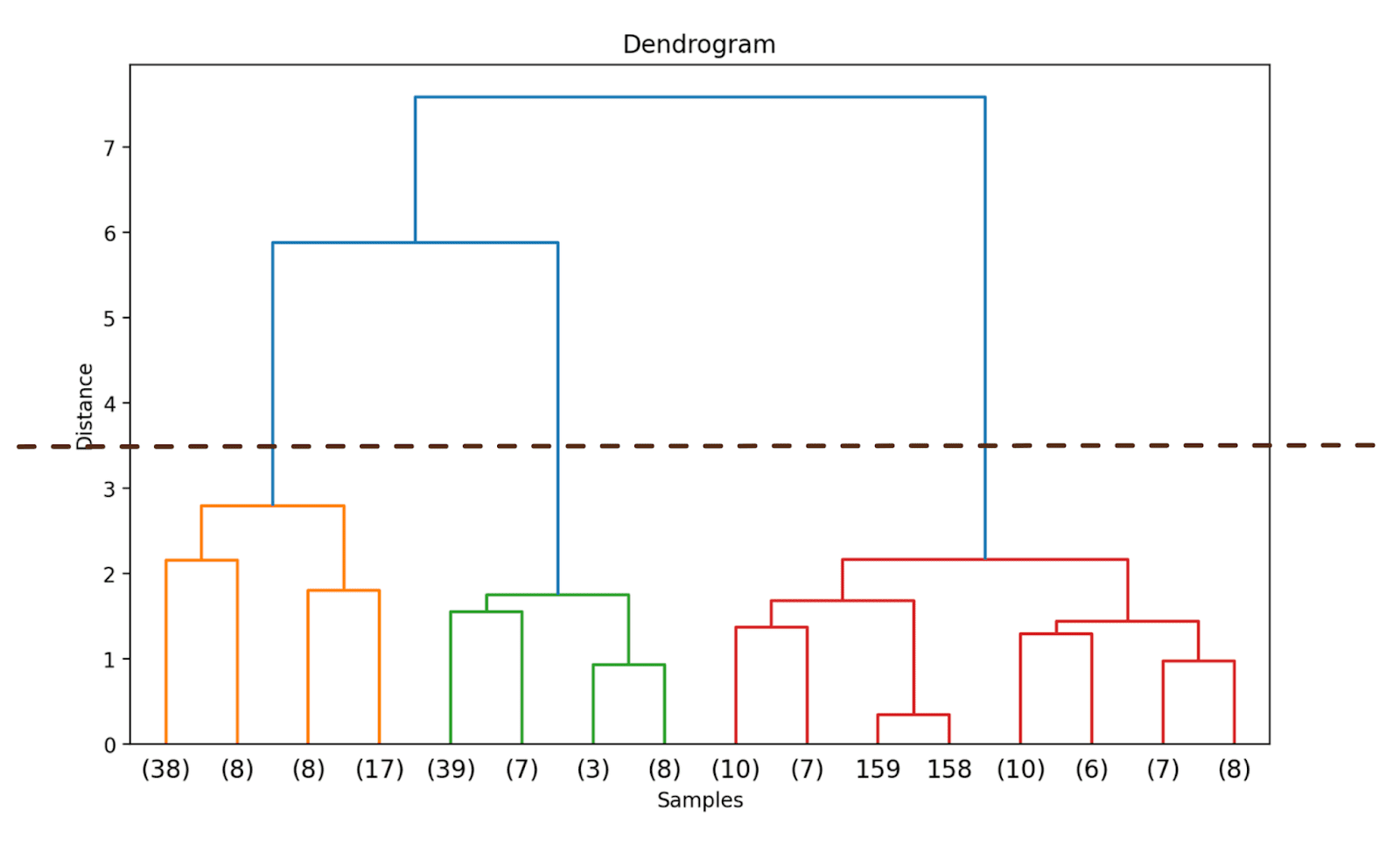
Doing so will truncate the dendrogram to incorporate solely these clusters that are inside 3 ranges from the ultimate merge.

Within the above dendrogram, you possibly can see that some information factors resembling 158 and 159 are represented individually. Whereas some others are talked about inside parentheses; these are not particular person information factors however the variety of information factors in a cluster. (okay) denotes a cluster with okay samples.

Step 4 – Determine the Optimum Variety of Clusters

The dendrogram helps us select the optimum variety of clusters.

We are able to observe the place the space alongside the y-axis will increase drastically, select to truncate the dendrogram at that time—and use the space as the brink to kind clusters.

For this instance, the optimum variety of clusters is 3.

Step 5 – Kind the Clusters

As soon as we now have selected the optimum variety of clusters, we are able to use the corresponding distance alongside the y-axis—a threshold distance. This ensures that above the brink distance, the clusters are not merged. We select a threshold_distance of three.5 (as inferred from the dendrogram).

We then use fcluster with criterion set to ‘distance’ to get the cluster task for all the information factors:

from scipy.cluster.hierarchy import fcluster

# Select a threshold distance primarily based on the dendrogram
threshold_distance = 3.5  

# Minimize the dendrogram to get cluster labels
cluster_labels = fcluster(linked, threshold_distance, criterion='distance')

# Assign cluster labels to the DataFrame
wine_df['cluster'] = cluster_labels

It’s best to now be capable of see the cluster labels (certainly one of {1, 2, 3}) for all the information factors:

print(wine_df['cluster'])

Output >>>
0      2
1      2
2      2
3      2
4      3
      ..
173    1
174    1
175    1
176    1
177    1
Title: cluster, Size: 178, dtype: int32

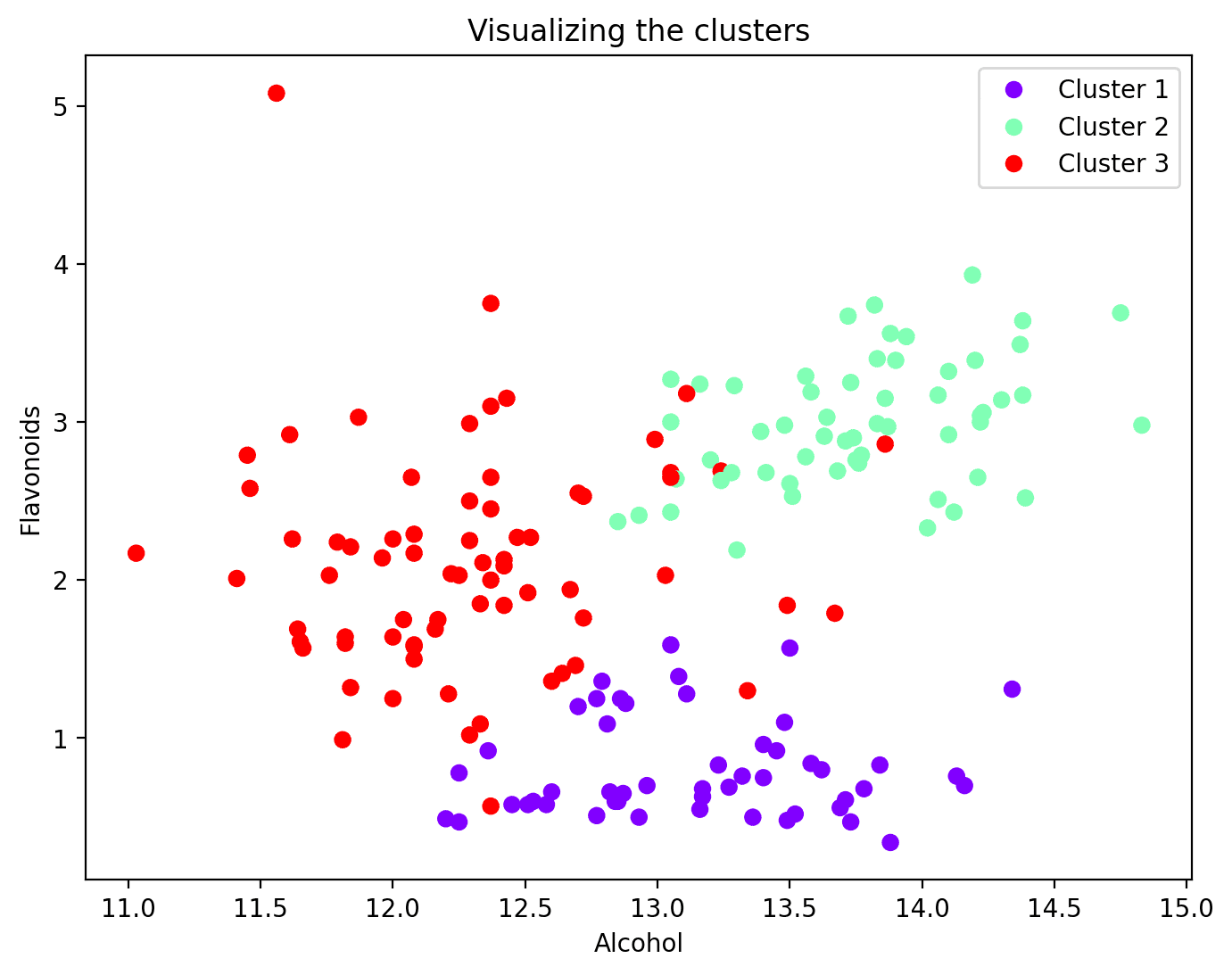
Step 6 – Visualize the Clusters

Now that every information level has been assigned to a cluster, you possibly can visualize a subset of options and their cluster assignments. This is the scatter plot of two such options together with their cluster mapping:

plt.determine(figsize=(8, 6))

scatter = plt.scatter(wine_df['alcohol'], wine_df['flavanoids'], c=wine_df['cluster'], cmap='rainbow')
plt.xlabel('Alcohol')
plt.ylabel('Flavonoids')
plt.title('Visualizing the clusters')

# Add legend
legend_labels = [f'Cluster {i + 1}' for i in range(n_clusters)]
plt.legend(handles=scatter.legend_elements()[0], labels=legend_labels)

plt.present()

Wrapping Up

And that is a wrap! On this tutorial, we used SciPy to carry out hierarchical clustering simply so we are able to cowl the steps concerned in higher element. Alternatively, you may also use the AgglomerativeClustering class from scikit-learn’s cluster module. Completely happy coding clustering!

References

[1] Introduction to Machine Studying

[2] An Introduction to Statistical Studying (ISLR)

Bala Priya C is a developer and technical author from India. She likes working on the intersection of math, programming, information science, and content material creation. Her areas of curiosity and experience embrace DevOps, information science, and pure language processing. She enjoys studying, writing, coding, and occasional! At present, she’s engaged on studying and sharing her information with the developer neighborhood by authoring tutorials, how-to guides, opinion items, and extra.